You want to combine these two equations into one equation with a single variable, solve it and then solve for the other variable An example on how to do this goes like this y − x = 3 → y = x 3 and we have y2 = x2 6x 9 Since x2 y2 =(graph 300x0 pixels, x from 6 to 5, y from 10 to 10, of TWO functions x/2 1 and x/2 3) You can put this solution on YOUR website!Question γ1f(x,y) = 37;
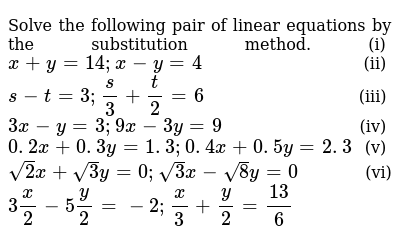
The Data In The Table Illustrate A Linear Function X 3 0 3 6
X-y=3 x/3+y/2=6 by elimination method
X-y=3 x/3+y/2=6 by elimination method-View more examples » Access instant learning tools Get immediate feedback and guidance with stepbystep solutions and Wolfram Problem Generator LearnX2y=3_2xy=1 Since 2y does not contain the variable to solve for, move it to the righthand side of the equation by subtracting 2y from both sides x=2y3_2xy=1 Replace all occurrences of x with the solution found by solving the last equation for x In this case, the value substituted is 2y3 x=2y3_2 (2y3)y=1




Show That The Lines 2x Y 3 0 3x 2y 2 0 And 2x 3y 23 0 Are Concurrent And Find The Point Of Concurrency
X 2 y 2 6 y 1x 3 y3 yy 3 y2 y 3 AB C D E 2 x 5 2 x 3 x x 5 x Question 40 Which from MATH at SMK Bukit Jalil This preview shows page 12 17 out of 18 pagesX^3 x^2 y x y^2 y^3 Extended Keyboard;180 x 3 6 150 y 3 7 49 a 3 b 2 8 4 a 4 b 3 c 9 45 x 5 y 3 10 50 x 6 y 4 11 64 r 2 s 6 t 5 12 144 r 8 s 6 t 2 13 (x 1) 2 14 (2 x 3) 2 15 4 (3 x − 1) 2 16 9 (2 x 3) 2 17 9 x 3 25 y 2 18 4 x 5 9 y 4 19 m 7 36 n 4 147 m 9 n 6 21 2 r 2 s 5 25 t 4 22 36 r 5 s 2 t 6 23 27 a 3 3 24 125 b 3 3 25 250 x 4
Click here👆to get an answer to your question ️ Solve the following pair of simultaneous equations x/3 x y/6 = 3;SOLUTION 13 Begin with x 2 xy y 2 = 1 Differentiate both sides of the equation, getting D ( x 2 xy y 2) = D ( 1 ) , 2x ( xy' (1)y) 2 y y' = 0 , so that (Now solve for y' ) xy' 2 y y' = 2x y, (Factor out y' ) y' x 2y = 2 x y, and the first derivative as The Questions and Answers of X Y =3 ,x/3 y/2=6?
Expand polynomial (x3)(x^35x2) GCD of x^42x^39x^246x16 with x^48x^325x^246x16;Free system of equations calculator solve system of equations stepbystepGraph of the equation 2x 3y = 4 and x y 3 = 0 Clearly two lines intersect at (1, 2) Hence x = 1 and y = 2 is the solution of the given system of equations



1




Mathematics Class 9th Chapter 4 Solution
Remainder of x^32x^25x7 divided by x3;To find the tenth term, I plug x, 3, and 12 into the Binomial Theorem, using the number 10 – 1 = 9 as my counter 12C9 ( x) 12–9 (3) 9 = (2) x3 (196) = x3 Find the middle term in the expansion of (4x – y)8 Since this binomial is to the power 8, there will be nine terms in the expansion, which makes the fifth term the middle oneQuotient of x^38x^217x6 with x3;



If X 3 Y 3 9 And X Y 3 Then What Is The Value Of X 4 Y 4 Quora
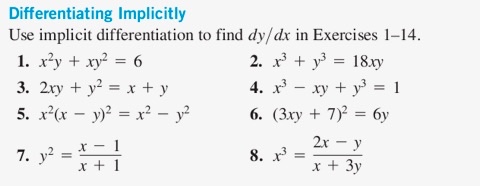



Use Implicit Differentiation To Find Dy Dx In Chegg Com
Are solved by group of students and teacher of Class 10, which is also the largest student community of Class 10 If the answer is not available please wait for a while and a community member will probably answer this soonCircle on a Graph Let us put a circle of radius 5 on a graph Now let's work out exactly where all the points are We make a rightangled triangle And then use Pythagoras x 2 y 2 = 5 2 There are an infinite number of those points, here are some examplesSlope intercept form is y=mxb Really, it is more like "Rise/Run Slope of a line from the yintercept form" If you want to know the xintercept form you can solve the equation for x y=2x4 would become x=1/2y2 Now plug in zero for y and you will have what x is equal to (2) The reason we use y=mxb is because the idea of rise/run no




Algebra Calculator Tutorial Mathpapa




If X Y 3 X Y 2 Then What Is The Value Of X 3 Y 3
To find the xintercept (s), substitute in 0 0 for y y and solve for x x 0 = − 2 x 3 2 0 = 2 x 3 2 Solve the equation Tap for more steps Rewrite the equation as − 2 x 3 2 = 0 2 x 3 2 = 0 − 2 x 3 2 = 0 2 x 3 2 = 0 Subtract 2 2 from both sides of the equation − 2 x 3 = − 2 2 x 3 = 2MATH 04 Homework Solution HanBom Moon Explain why f(x;y) = 1 xln(xy 5) is differentiable at (2;3) Then find the linearization L(x;y) of the function at that point x y = 3 x/3 y/2 = 6 LCM = 6 x/3 × 6 y /2 × 6 = 6 × 6 2x 3y = 36 (x y = 3) × 2 2x 3y = 36 (2x 2y = 6) 5y = 30 y = 6 x y = 3 x 6 = 3 x = 9
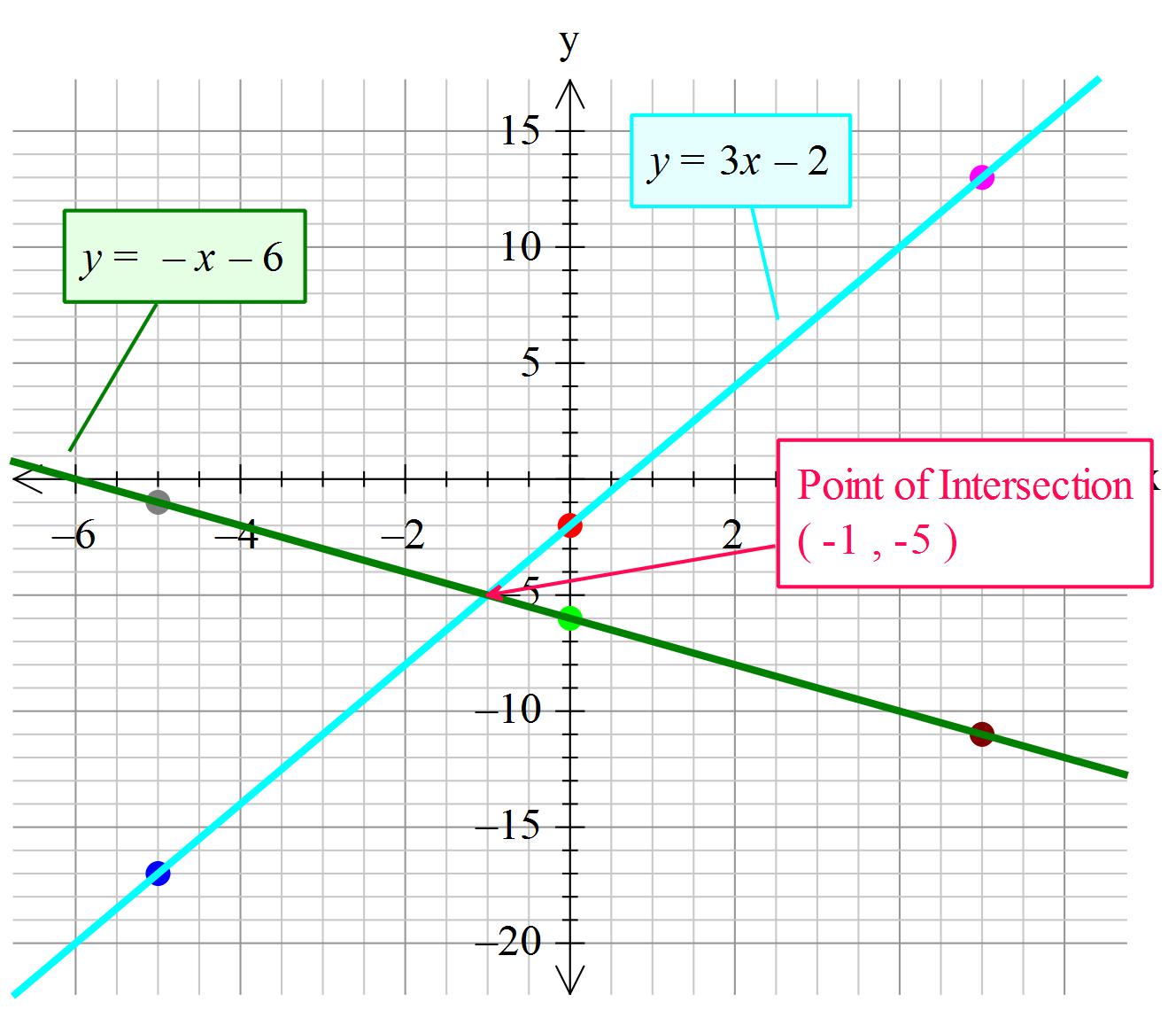



How Do You Solve The System Of Equations By Graphing Y 3x 2 X Y 6 Socratic




Sqrt3x Sqrt8y0 Dfracx3dfracy2 See How To Solve It At Qanda
Write cos(x 3) as cos(x^3) 3 Write e x lnx as e^xln(x) 6 Ensure that the input string is as per the rules specified above An online derivative calculator that differentiates a given function with respect to a given variable by using analytical differentiation A useful mathematical differentiation calculator to simplify the functionsAnd γ4f(x,y) = SHOW ALL WORK A) Find Points (x,y), If Any, Where Curves γ1and γ3 Are Tangent B)Find Points (x,y), If Any, Where Curves γ2 And γ3 Are Tangent C) Find The Minimum And Maximum Values Of F(x,y) Subject To The Constraint (x−3)2y2−6y= 0Solve for x Use the distributive property to multiply xy by x^ {2}xyy^ {2} and combine like terms Use the distributive property to multiply x y by x 2 − x y y 2 and combine like terms Subtract x^ {3} from both sides Subtract x 3 from both sides Combine x^ {3} and x^ {3} to get 0 Combine x 3 and − x 3 to get 0
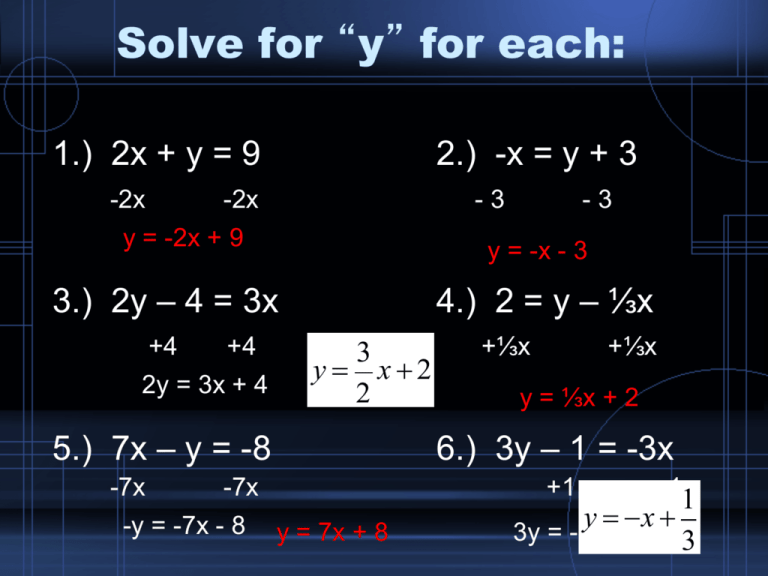



Document




Solve The Following Simultane See How To Solve It At Qanda
DEFINITION A differential equation is separable if it is of the form y'=f (x,y) in which f (x,y) splits into a product of two factors, one depending on x alone and the other depending of y alone Thus each separable equation can be expressed in the form y'=Q (x)R (y), where Q and R are given functions When R (y)0 we can divide by R (y) and It is important that when you sub into y=3x^2 the y value will always be negative make sure you do (3) (x^2) , so you square the x first, which will never be negative, and then multiply that by 3 So any point in your list with a positive yPair of Linear Equations in Two Variables X Y=3 ,X?3Y?2=6 Share with your friends




X 2 2y 3 1 And X Y 3 3 Find X And Y Values Using Elimination And Substitution Method Youtube




2 X 2 3y 1 6 And 3 X 2 Y 0 Problem Set 1 Q6 1 Of Linear Equation In Two Variables Youtube
Y/3 x y/2 = 6Implicit differentiation can help us solve inverse functions The general pattern is Start with the inverse equation in explicit form Example y = sin −1 (x) Rewrite it in noninverse mode Example x = sin (y) Differentiate this function with respect to x on both sides Solve for dy/dxSOLUTION Solve this system of equations by graphing x 2y = 2 x 2y = 6 You can put this solution on YOUR website!




X Y 3 X 3 Y 2 6 Novocom Top




Systems Of Equations With Substitution Y 1 4x 100 Y 1 4x 1 Video Khan Academy
Graph{x^33x^29x5 1459, 1726, 856, 736} FIrst determine the interval of definition, then the behavior of first and second derivatives and the behavior of the function as \displaystyle{x} Example 17 Solve the pair of equations 2/𝑥 3/𝑦=13 5/𝑥−4/𝑦=−2 2/𝑥 3/𝑦=13 5/𝑥−4/𝑦=−2 So, our equations become 2u 3v = 13 5u – 4v = –2 Hence, our equations are 2u 3v = 13 (3) 5u – 4v = – 2 (4) From (3) 2u 3v = 13 2u = 13Answer to Find all the local maxima, local minima, and saddle points of the function f (x, y) = x^3 y^3 6 x^2 9 y^2 6 By signing up,




Example 18 Solve 5 X 1 1 Y 2 2 6 X 1 3 Y 2 1 Examples
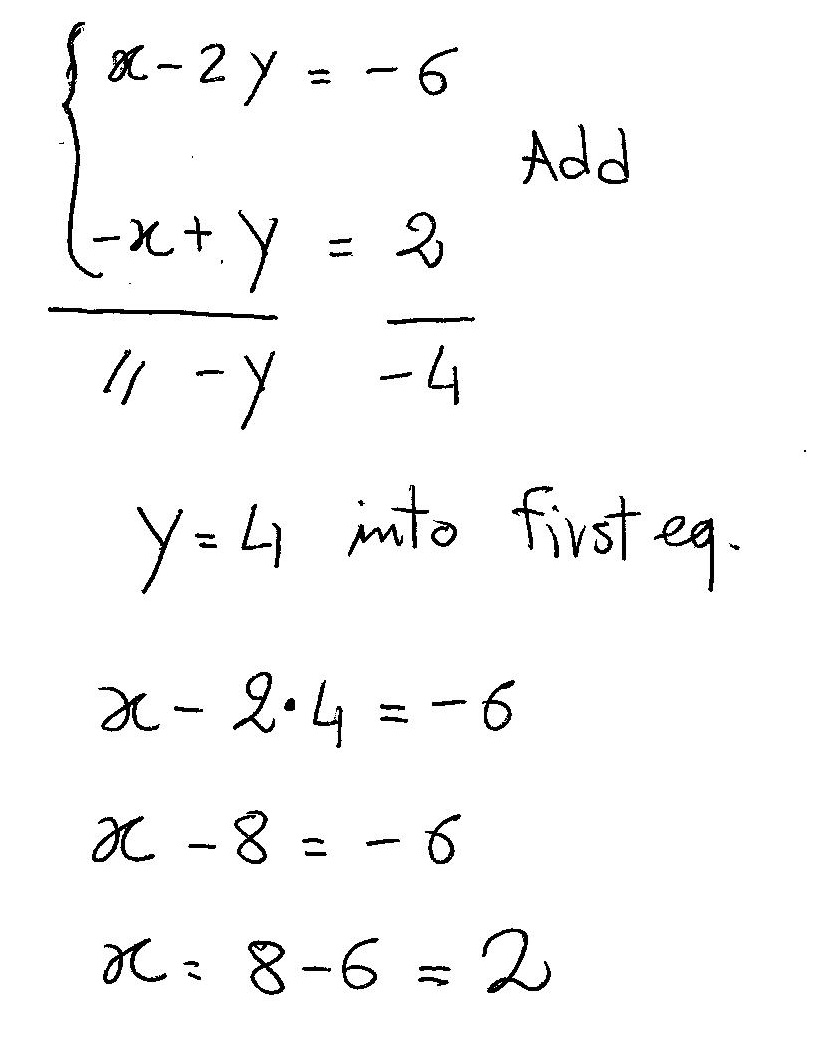



How Do You Solve X 2y 6 And X Y 2 Socratic
To find the xintercept (s), substitute in 0 0 for y y and solve for x x 0 = 3 x 2 6 0 = 3 x 2 6 Solve the equation Tap for more steps Rewrite the equation as 3 x 2 6 = 0 3 x 2 6 = 0 3 x 2 6 = 0 3 x 2 6 = 0 Subtract 6 6 from both sides of the equation 3 x 2 = − 6 3 x 2 = 6= ntn−1f(x,y) (3) Setting t = 1 in the Equation (3) x ∂f ∂x y ∂f ∂y = nf(x,y) 5 Find the directional derivative of the function f(x,y,z) = p x2 y2 z2 at the point (1,2,−2) in the direction of vector v = h−6,6,−3i Solution We first compute the gradient vector at (1,2,−2) ∇f(x,y,z) = * x pIn order to graph these equations, we need to solve for y for each equation




If X Y 3 Xy 2 Find The Value Of X3 Y3 Brainly In



If X Y 6 And 3x Y 4 Then What Is X Y Equal To Quora
Y = x – 3 Substituting y = x – 3 in (ii), we get `x/3 (x −3)/2` = 6 ⇒2x 3 (x – 3) = 36 ⇒2x 3x – 9 = 36 ⇒x = `45/5` = 9 Now, substituting x = 9 in (i), we have 9 – y = 3 ⇒y = 9 – 3 = 6 Example 18 Solve the following pair of equations by reducing them to a pair of linear equations 5/(𝑥 −1) 1/(𝑦 −2) = 2 6/(𝑥 −1) – 3/(𝑦 −2) = 1 5/(𝑥 − 1) 1/(𝑦 − 2) = 2 6/(𝑥 − 1) – 3/(𝑦 − 2) = 1 So, our equations become 5u v = 2 6u – 3v = 1 Thus, ourHow to Check Your Answer with Algebra Calculator First go to the Algebra Calculator main page Type the following First type the equation 2x3=15 Then type the @ symbol Then type x=6 Try it now 2x3=15 @ x=6



If X Y 2 Then What Is The Value Of X Y 6xy Quora




Solve For X And Y X Y 3 X 3 Y 2 6 Brainly In
Plot y = x^2 from x = 3 to x = 3 Plot x^2 y^2 = 4 from x = 2 to x = 2 Plot y = sin(x) from x = 0 to x = 2 pi Advanced Plot y = 3x^2 1 and y = 2x^3 4 from x = 3 to x = 3, y = 17 to y = 17 with an aspect ratio of 1 2Cho các đa thức B = −8xy3 xy2 −4x2y2 B = 8 x y 3 x y 2 4 x 2 y 2 C = x3 4x3y − 6xy3 − 4xy2 5x2y2 C = x 3 4 x 3 y 6 x y 3 4 x y 2 5 x 2 y 2 Hãy tính a) A – B – C b) B A C c)C – A – B Trả Lời Hỏi chi tiết it can be done with any method but the answer remains same i m doing with SUBSTITUTION method By substitution method xy=3=> x=y3 x/3 y/2=6 Substituting in ( x/3y/2=6) => (y3)/3y/2=6 => (2y63y)/6=6 =>2y63y=36




X Y 8 2 X 2y 14 3 3x Y



If X 3 Y 3 9 And X Y 3 Then What Is The Value Of X 4 Y 4 Quora
Subtracting (A){(B) we get ‚(x ¡ 2y) = 0, so either ‚ = 0 or x = 2yBut ‚ = 0 would give x = y = z = 0, and f(0;0;0) = 0 is obviously not the maximumTherefore we work with x = 2y Subtracting (B){ we get ‚(2y¡3z) = 0, and since we already discarded the case ‚ = 0 we are left with z = 2 3 y Using the results in the two frames into (D) we get463 Explain the significance of the gradient vector with regard to direction of change along a surface;464 Use the gradient to find the tangent to a level curve of a given function
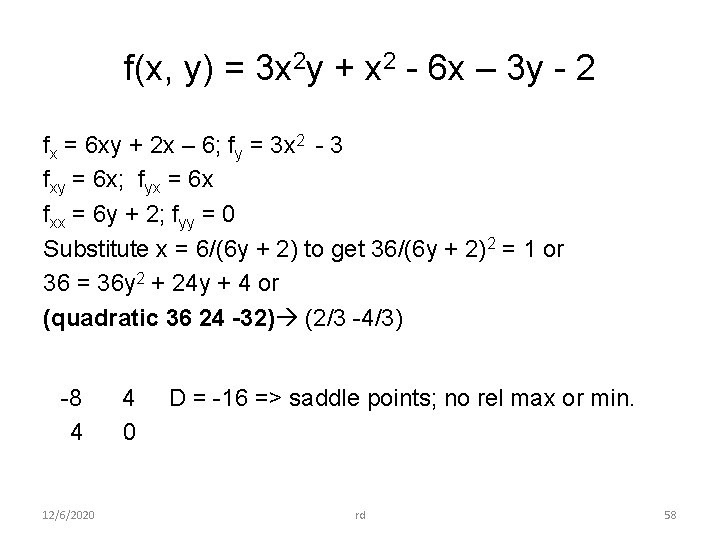



Differential Calculus Concepts Problems 126 Rd 1 Matrix




Ex 6 3 11 Solve 2x Y 4 X Y 3 2x 3y 6
462 Determine the gradient vector of a given realvalued function;Econ 1A Ramu Ramanathan Spring 03 Answers to Exam #2 I Let X and Y be two random variables, with means µ x and µ y, Var(X) = 2 = E(X σX 2) − 2, Var(Y) = = E(Y µX 2 σY 2) − 2, and Cov (X, Y) = µY σXYNow make the transformations U = X Y, and V = X − Y (a) (3 points) Derive E(U) and E(V) in terms of µX and µYShare It On Facebook Twitter Email 1 Answer 0 votes answered by AmirMustafa (599k points) selected by Vikash Kumar Best answer The given system of equations is




3x 2 5y 3 2 And X 3 Y 2 13 6 Solve Using Substitution Method Youtube




Show That The Lines 2x Y 3 0 3x 2y 2 0 And 2x 3y 23 0 Are Concurrent And Find The Point Of Concurrency
(x y) 3 = 7 3 (6) = 25 x y = 25 3 Next, factor the second given equation in conjunction with the result found above, to get an equation for y in terms of x x 2 y x y 2 = x y (x y) = 6 x y = 6 x y x y = 6 25 3 y = 6 25 3 x Substitute this expression for y into the first given equation to eliminate y to get an easily solvable equation for x x 3 y 3 = 7 x 3 (6 25 3 x) 3 = 7 Explanation We use implicit differentiation as follows differentiating x2 y2 = 1, we get 2x 2y dy dx = 0 ie dy dx = − x y and differentiating it further 2 2 dy dx dy dx y ⋅ d2y dx2 } = 0 or 2 2 dy dx2 2yd2y dx2 = 0 or 2 2 x2 y2Namely, the parenthetical factor x – yThis binomial may be different from what I'm used to seeing referred to as being a "factor", but the factorization process works just the same for this expression as it did for every




The Factors Of X 3 X 2y X Y 2 Y 3 Are A X Y X 2 X Y Y 2 B X Y X 2 X Y Y 2 C Youtube




Standard Form Examples 3x Y 5 2x Y 10 X Y 6 Ppt Download
x – y = 3, x/3 y/2 = 6 linear equations in two variables;To find the point of intersection of the two lines, we need to solve the system of equations x y = 3 and 5 x 2 y = 22 simultaneously Equation x y = 3 can be solved for x to give x = 3 y Substitute x by 3 y in the equation 5 x 2 y = 22 and solve for y5 (3 y)={(xy)^3/2×(xy)^3/2× 1/(xy)^1/2 ×(xy)^3/2}^6 ={(xy)×(xy)^3}^6 ={(x^2y^2)(xy)^2}^6 =(x^2y^2)^6(xy)^12 , Answer




Consider The Function F X Y 3 X 3 Y 2 Find Chegg Com




Solve The Following Systems By Gaussian Elimination Chegg Com
Apply the rules of exponents (2x 3 y 4) 5 Solution Within the parentheses there are three factors 2, x 3, and y 4 According to Rule 2 we must take the fifth power of each one But to take a power of a power, we multiply the exponents Therefore, (2x 3 y 4) 5 = 2 5 x 15 y Problem 7 Apply the rules of exponentsLearning Objectives 461 Determine the directional derivative in a given direction for a function of two variables;This expression may seem completely different from what I've done before, but really it's not The two terms, 2(x – y) and –b(x – y), do indeed have a common factor;



How To Solve The Simultaneous Equations X 2 Y 2 36 And X 2y 6 Quora




Graph Graph Inequalities With Step By Step Math Problem Solver
X y 3 = xy 2y x 3 2x 2 Now differentiate both sides of the equation, getting D ( x y 3) = D ( xy 2y x 3 2x 2) , D ( x) D (y 3) = D ( xy) D ( 2y) D ( x 3) D ( 2x 2) , (Remember to use the chain rule on D (y 3) ) 1 3 y 2 y' = ( xy' (1)y) 2 y' 3x 2 4x, so that (Now solve for y' ) 1 y 3x 2 4x = 3 y 2 yCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, musicSystems of equations 1 Solve the system 5 x − 3 y = 6 4 x − 5 y = 12 \begin {array} {l} {5x3y = 6} \\ {4x5y = 12} \end {array} 5x−3y = 6 4x−5y = 12 See answer › Powers and roots 2 Expand for x




Solutions To Implicit Differentiation Problems



How To Solve For X And Y In X Y 5 And Xy 6 Quora




Consider The Surface Given By Z Xy 3 X 2y Find Chegg Com




If 2x 3y 12 And Xy 6 Find The Value Of 8x 3 27y 3



Q Tbn And9gcqtchv4nfv 5y1vsuv4syhh0eeanjbyt8r7tqframh6dhhqrj Usqp Cau




X Y 3 And X 3 Y 2 6 Solve The Following Pair Of Linear Equations By The Elimination Method And Brainly In




Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Download Free Pdf




Solution Of X Y 3 And X 3 Y 2 6 By Elimination Method Brainly In




X Y 3 X 3 Y 2 6 Youtube



If X 3 Y 3 9 And X Y 3 Then What Is The Value Of X 4 Y 4 Quora



How Do You Solve The System 2 X 4 Y 6 3x 2 Y 3 13 Socratic




Give The General Solution To Y 3x 3 Y 2 Xy Chegg Com



Solve 5 X 1 1 Y 2 2 And 6 X 1 3 Y 2 1 Studyrankersonline
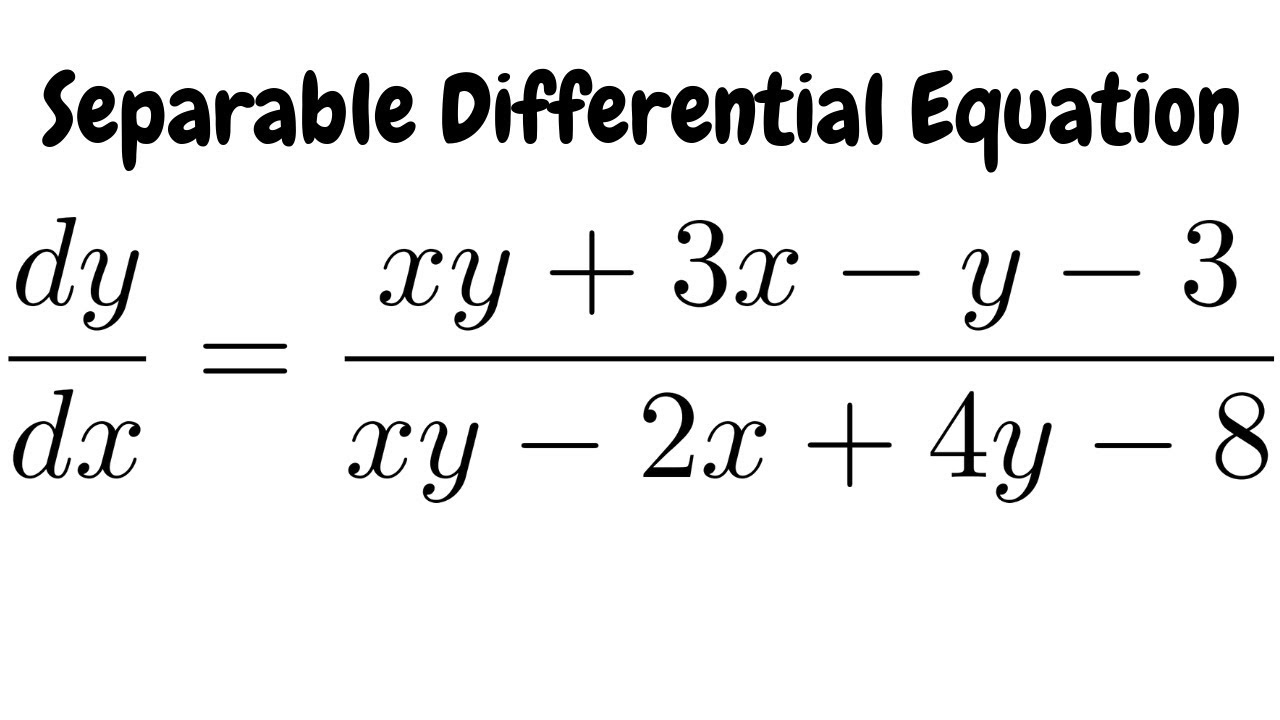



Separable Differential Equation Dy Dx Xy 3x Y 3 Xy 2x 4y 8 Youtube




Solve X 1 3y 3 X 1 2y X 1 Y 6 Log X 1 Mathematics Stack Exchange



2x 3y 0 3x 4y 5 By Elimination Method




X Y 3 X 3 Y 2 6 Brainly In




X Y 3 X 3 Y 2 6 Elimination Method Brainly In




Solve Each Differential Equation Dy Dx 5y E 3x Chegg Com




Discuss The Maxima And Minima Of The Function U X 3y 2 1 X Y Answer Mathematics 1 Question Answer Collection



Solved Find The Common Solution Of Each Using The Elimination Substitution And Graphical Method 2x Y 2 X 3y 36 2 3x Y 6 X Y 6 3 Course Hero
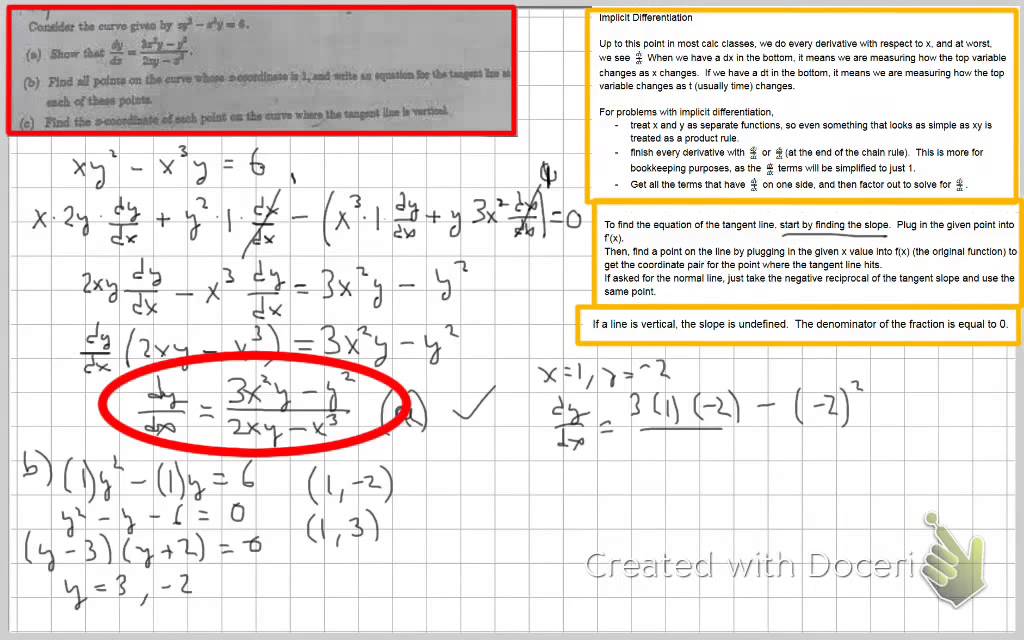



Ap Calculus Consider Curve Given By Xy 2 X 3 Y 6 Find Dy Dx And Tangent Lines Youtube




X Y 3x 3 Y 2 6solve For X And Ylinear Equations In Two Variables Brainly In
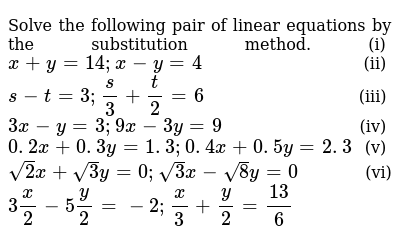



The Data In The Table Illustrate A Linear Function X 3 0 3 6



If 2 X 3 Y 6 Z Then What Is The Value Of 1 X 1 Y 1 Z Quora




Algebra Calculator Tutorial Mathpapa
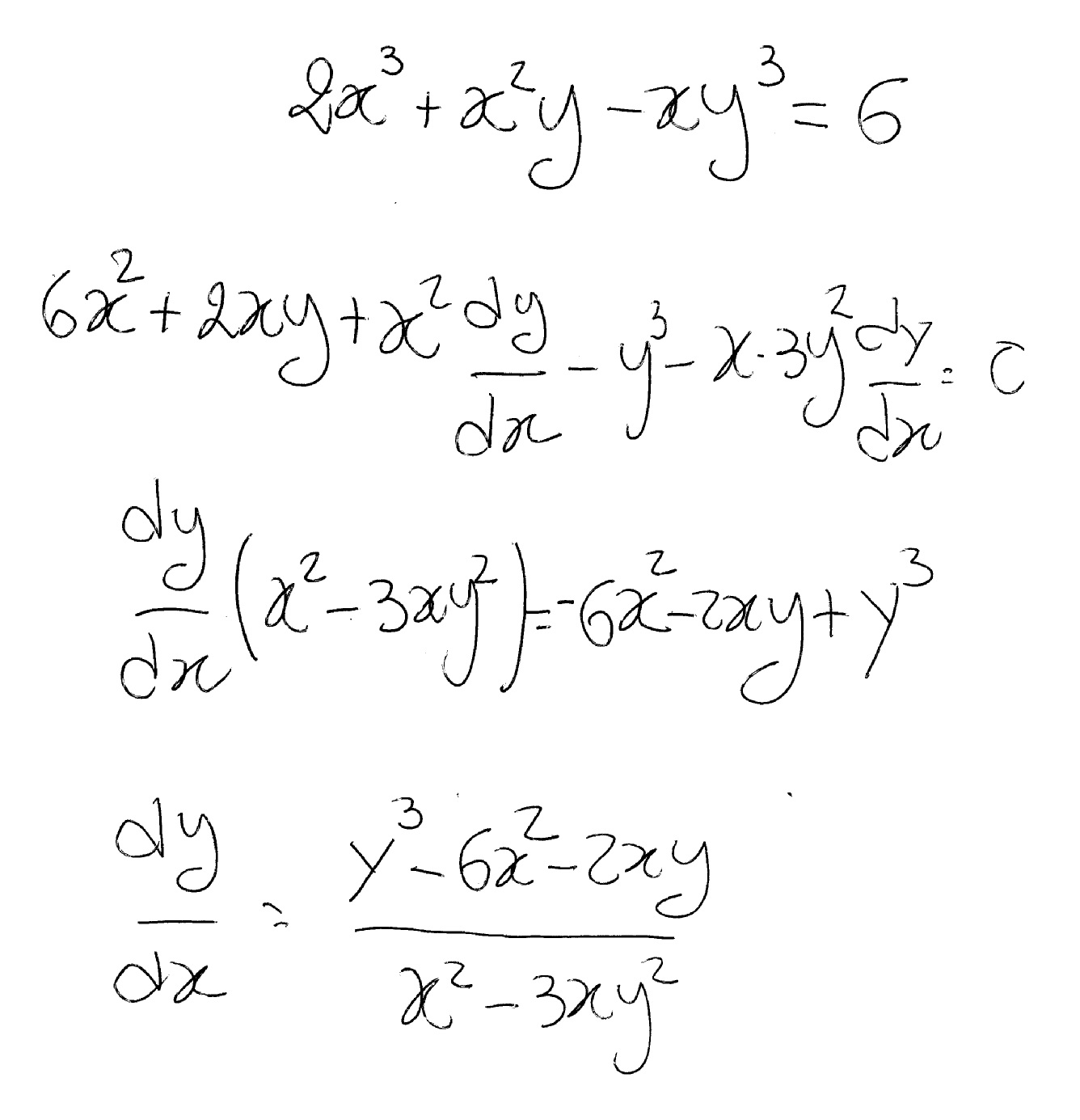



How Do You Find Dy Dx By Implicit Differentiation For 2x 3 X 2 Y Xy 3 6 Socratic




X Y 3 X 3 Y 2 6




Standard Form Examples 3x Y 5 2x Y 10 X Y 6 Ppt Download



How Do You Solve X 2 Y 3 6 And X 3 Y 2 12 Socratic




The Value Of X Y 2 3 X Y 3 2 Root X Y Root X Y 3 6 Is Brainly In




X 2 2y 3 1 Amp X Y 3 3 Solve By Eliminations Or Substitution Method Brainly In



How To Factorise 3 X Y 2 2 X Y Quora




Solve For X And Y 5 X 1 Y 2 6 X 3 Y 1 Brainly In




X 2 2y 3 1 X Y 3 3 Solve The Given Equation Using Elimination And Substitution Method Youtube




Solve X Y 3 And X 3 Y 2 6 By Substituting Methos Scholr




For The Following Data X Y 3 8 5 8 6 2 3 6 1 4 4 Chegg Com




Solve The Following Pair Of L See How To Solve It At Qanda




Answered Y 4 3 1 2 12x 10y 4 3 5 2 Bartleby




Example 1 If X 1 Y 2 3 1 Find X And Y Class 11




Ex 3 6 1 V And Vi 7x 2y Xy 5 8x 7y Xy 15



Q Tbn And9gcryl6g3sfxmqcga1 Fsavvgw Ex1efh3la10uve9fzhff P98 Usqp Cau




Solve Equations Using Substitution Method 2x Y 3 And 4x Y 3




Solve The Following Pair Of Equations By Reducing Them To A Pair Of Linear Equations 5x 1 1y 2 2 And 6x 1 3y 2 1




If X 3 2 3 2 And Y 1 The Value Of X Y X 3y Is A 5 5 4 B 5 6 4 C 6 4 5 D 6 4 5 Brainly In




6 X Y 7 X Y 3 1 2 X Y 1 3 X Y




X Y 3 X 3 Y 2 6 Elimination Method Brainly In



Systems Of Linear Equations




Systems Of Equations With Graphing Article Khan Academy




If X Y 6 And 3x Y 4 Then What Is X Y Equal To Quora




Exact Equations Example 3 Video Khan Academy



Www Tau Ac Il Levant Ode Solution 6 Pdf




Simplify X Y 3 X Y 3 6y X 2 Y 2




Ex 3 6 1 V And Vi 7x 2y Xy 5 8x 7y Xy 15




Solve The Pair Of Equations 2 X 3 Y 13 5 X 4 Y 2 Youtube




How Do You Solve The System 4x 2y 6 And X Y 3 Socratic



Secure Media Collegeboard Org Digitalservices Pdf Ap Apcentral Ap15 Calculus Ab Q6 Pdf




Use Implicit Differentiation To Find Dy Dx In Chegg Com



Solve The Following Systems Of Equations 6 X Y 7 X Y 3 1 2 X Y 1 A X Y Where X Y 0 And X Y 0 Sarthaks Econnect Largest Online Education Community



How Do You Solve The System 3x 2y 6 And 3x Y 12 By Graphing Socratic




15 62 1 0 30 8 2 16 3 2 6 Are Parallel See Chegg Com
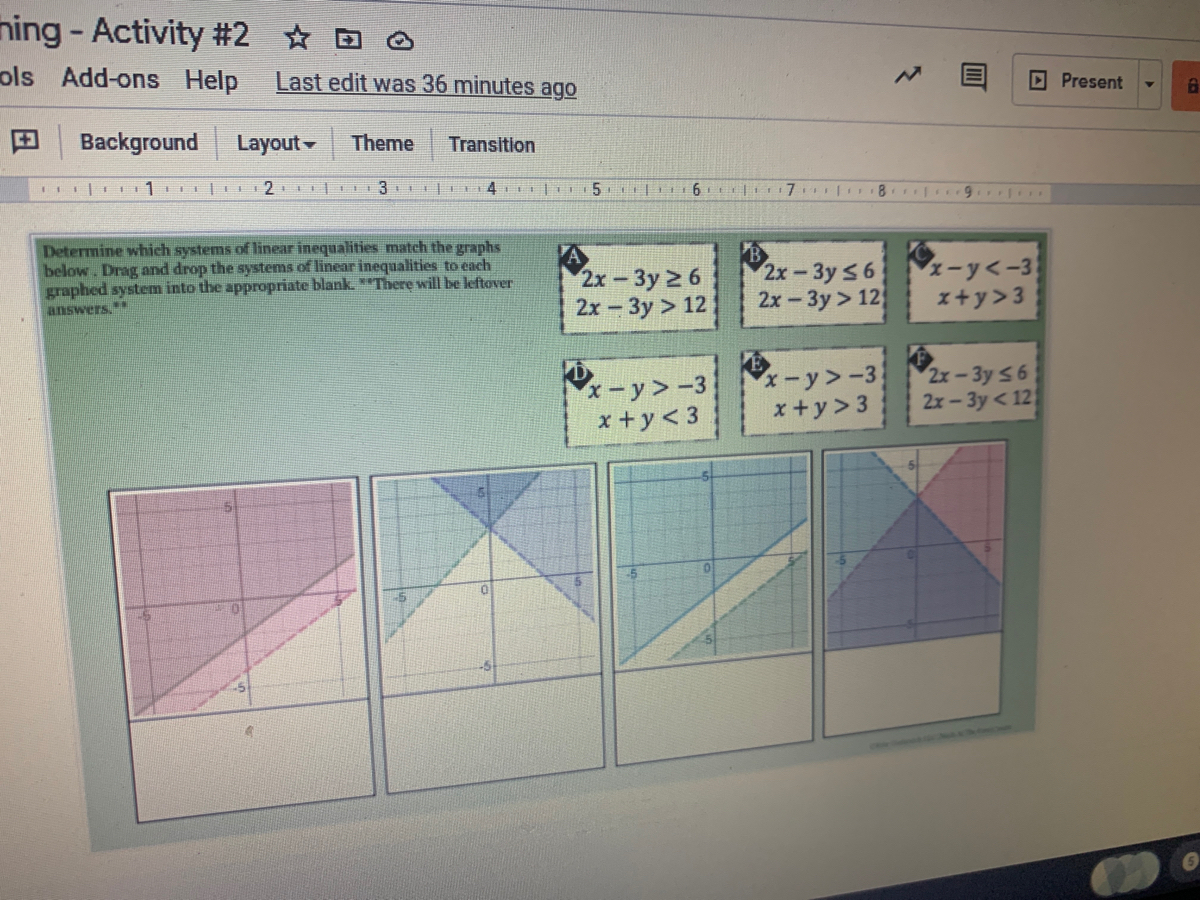



Answered 2x 3y 2 6 2h Zu 12 B 2x 3y 56 Bartleby




Each Other Exercise 33 Solve See How To Solve It At Qanda



Graph Graph Equations With Step By Step Math Problem Solver



Implicit Differentiation 1 Xy X 2y 2 6 2 Chegg Com
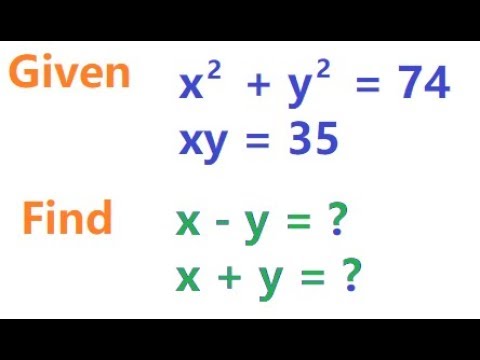



X 2 Y 2 74 And Xy 35 Find X Y And X Y 2x 3y 14 And Xy 8 Find 4x 2 9y 2 Youtube




Solve The Following System Of Equations 27 X Y 15 X Y 2 And 30 X Y 1 X Y 3 Mathematics Topperlearning Com X68shsoo




Solve For X And Y 40 X Y 2 X Y 5 And 25 X Y 3 X Y 1 Mathematics Topperlearning Com Idbi1itt




Misc 16 Solve Equations 2 X 3 Y 10 Z 4 4 X 6 Y 5 Z 1




न म नल ख त सम करण क प रत स थ पन व ध द व र हल क ज ए X Y 3




X 2 Y 2 3 6 Xy 12 Novocom Top



Solve The Following Systems Of Equations 6 X Y 7 X Y 3 1 2 X Y 1 A X Y Where X Y 0 And X Y 0 Sarthaks Econnect Largest Online Education Community



0 件のコメント:
コメントを投稿